El nuevo algoritmo de la compañía de transportes UPS puede trazar rutas más eficientemente que sus conductores. Ahora sólo falta convencer de ello a los conductores.

Leer aquí la noticia…

Los sistemas monetarios terrícolas suelen ser de tipo canónico. Eso significa que dada una cantidad de dinero a devolver, el algoritmo voraz que consiste en elegir primero la moneda de mayor valor posible que sea menor o igual que la cantidad a devolver, y aplicar el mismo algoritmo a la cantidad restante, iterativamente, nos da el mínimo número de monedas con el que podemos devolver la cantidad.

Contrariamente a lo que la mayoría de la gente piensa, en Marte hay vida inteligente. Tienen una sociedad altamente desarrollada, pero un curioso sistema monetario. Tienen monedas y billetes, como nosotros. El billete más pequeño es el papelín. Y sus monedas tienen cinco denominaciones. La más pequeña es la china, y un papelín vale 100 chinas. El resto de monedas son:

• 1 guijarro = 3 chinas
• 1 piedra = 11 chinas
• 1 pedrusco = 22 chinas
• 1 menhir = 47 chinas

Monedero marciano con chinas, guijarros y piedras

Por ejemplo, el mínimo número de monedas con valor igual a un papelín es cuatro: dos menhires y dos guijarros.

La entrada del problema consiste en una o más líneas. Cada línea contiene el precio de un artículo en chinas, comprendido entre 1 y 100, ambos incluidos. Para cada artículo el programa debe escribir una línea que describa el mínimo número de monedas necesarias para devolver el cambio, si se paga el artículo con un papelín.

Ejemplo de entrada:

77
34
99
57
13

Ejemplo de salida:

0 menhires, 1 pedrusco, 0 piedras, 0 guijarros, 1 china
0 menhires, 3 pedruscos, 0 piedras, 0 guijarros, 0 chinas
0 menhires, 0 pedruscos, 0 piedras, 0 guijarros, 1 china
0 menhires, 1 pedrusco, 1 piedra, 3 guijarros, 1 china
1 menhir, 1 pedrusco, 1 piedra, 2 guijarros, 1 china

Marciano arruinado

Fuente: aquí (fuente “desaparecida”; accesible en la waybackmachine)

“Last year, a group of us were lucky enough to visit the U.K. Prime Minister’s residence at 10 Downing Street, as part of the Silicon Valley Comes to the U.K. initiative. While there, we asked about some of the paintings on the wall. When we got to a large portrait of a regally dressed woman, our host said “and of course, that’s Lady Lovelace.” So much of world history leaves out or minimizes the contributions of women, and so “of course” most of us had no idea who she was. You can imagine our surprise when we learned she was considered by some to be the world’s first computer programmer—having published the first algorithm intended for use on Charles Babbage’s Analytical Engine…”

[Seguir leyendo]

Ada Byron, Condesa de Lovelace

Para ganar a ‘Piedra, papel o tijera’, hace falta conocer bien la psicología de tu adversario:

o hacer algo de trampa:

En cualquier otro caso, no será posible diseñar una estrategia ganadora. Formalicemos un poco el juego: Mediante matrices se pueden representar diversos juegos como el que inventaron Bob y Alice (ver entrada) o como ‘Piedra, papel o tijera’. Supongamos que dos jugadores, llamados Row y Column, deciden jugar a ‘Piedra, papel o tijera’. La ganancia del jugador Row (y equivalentemente la pérdida del jugador Column) puede representarse con la siguiente matriz.

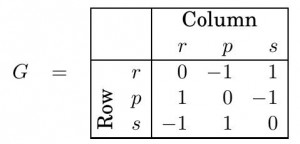
Las letras ‘r’, ‘p’ y ‘s’, se corresponden con las jugadas piedra (rock), papel (paper), tijera (scissors). Así, la entrada 1 de la fila ‘p’ y columna ‘r’ indica que si Row elige papel y Column piedra, entonces Row gana un punto.

¿Existe alguna estrategia ganadora para este juego? Es decir, ¿puede alguno de los jugadores asegurarse la victoria a la larga si juega óptimamente? Obviamente, si Row siempre elige la misma jugada, por ejemplo piedra, Column se percatará de su inocente estrategia, acabará sacando siempre papel y ganándole. Conviene por tanto despistar lo máximo posible al oponente eligiendo las jugadas de manera aleatoria. En clase confirmaremos el pensamiento intuitivo que nos dice que si los dos juegan lo mejor posible, es decir maximimizan el valor esperado de su ganancia (en este caso eligiendo al azar entre las tres jugadas), a la larga terminarán en empate. Lo mismo ocurrirá si introducimos dos jugadas más, ‘lagarto’ y ‘Spock’:

Imagina ahora que se obliga a Row a anunciar públicamente su estrategia (es decir la probabilidad con que elegirá piedra, papel y tijera) y Column puede elegir la suya en función de la de Row. ¿Se verá Row perjudicado por esta nueva regla del juego?

Y, ¿qué pasaría si en vez de ‘Piedra, papel o tijera’ o ‘Piedra, papel, tijera, lagarto o Spock’ , consideráramos un juego con la siguiente matriz?

¿Existe ahora una estrategia ganadora para alguno de los jugadores?

Trataremos este tipo de juegos en clase y veremos que se pueden obtener respuestas a estas preguntas mediante programación lineal.

“Divide y vencerás” (“divide and conquer” en inglés) es una de las estrategias que estudiaremos en la asignatura para la resolución de problemas.

Intentaremos no quedarnos a medio camino y después de “dividir” procuraremos “vencer”.

“We already have quite a few people who know how to divide, so essentially we’re now looking for people who know how to conquer.”

Cada nodo izquierdo de la figura representa a un chico y cada nodo derecho una chica. Hay un arco conectando dos personas si existe atracción mutua. Por ejemplo a Al le gustan todas las chicas y Al gusta a todas las chicas. ¿Es posible emparejar a todos de tal manera que todos estén contentos con su pareja? Es decir ¿existe el emparejamiento perfecto (perfect matching)?

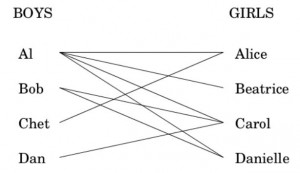
Este problema puede “transformarse”, en otras palabras “reducirse”, a un problema de flujo máximo en una red. El problema de flujo máximo consiste en calcular cuál es flujo máximo que puede producir un nodo fuente y alcanzar el nodo sumidero sin violar las capacidades de los arcos de la red. En las clases de Algoritmia Básica veremos que este problema puede resolverse de manera eficiente mediante un problema de programación lineal. La reducción del problema del emparejamiento perfecto es sencilla: simplemente hay que transformar el grafo inicial por uno similar con un nodo fuente “s” y un nodo sumidero “t”, dirigir todos los arcos en la dirección de las chicas y asignar una capacidad de uno a todos los arcos.

Habrá un emparejamiento perfecto si y sólo si el flujo máximo es igual al número de parejas deseado, es decir, en nuestro caso igual a 4. ¿Puedes encontrar ese emparejamiento?  o ¿siempre habrá alguien descontento?

Fuente: Algorithms, S. Dasgupta, C. H. Papadimitriou, U. V. Vazirani. Mc Graw-Hill, 2008.

Un avión de carga tiene tres compartimentos para almacenar su carga, frontal, central y trasero, con los siguientes límites máximos de capacidad, en peso y en volumen:

Compartimento  Peso (Tm)  Volumen (m3)
Frontal              10          6800
Central              16          8700
Trasero               8          5300

Además, para mantener el balance adecuado del avión, el peso de la carga en los tres compartimentos debe mantener la misma proporción que sus límites de capacidad de carga en peso.

Para el siguiente vuelo, se dispone de las siguientes mercancías a embarcar:

Mercancía   Peso (Tm)   Volumen (m3/Tm)  Valor (€/Tm)
M1                18              480            310
M2                15              650            380
M3                23              580            350
M4                12              390            285

El objetivo es determinar qué cantidad de cada mercancía debe embarcarse y cómo distribuirla en los compartimentos de forma que el valor total de la mercancía embarcada sea máximo.

Puede suponerse que cada mercancía puede fraccionarse, si se precisa, en cualquier proporción y que puede repartirse entre dos o más compartimentos, si se desea.

Nuestro avión

Solución

• Hay que decidir qué cantidad de cada mercancía debe ponerse en cada compartimento. Sea:

x_ij el número de toneladas de mercancía Mi (i=1,2,3,4) que va a ponerse en el compartimento j (j=1 para Frontal, j=2 para Central y j=3 para Trasero), con x_ij ≥ 0 para i=1,2,3,4; j=1,2,3.

• No puede cargarse más cantidad de cada mercancía que la disponible:

x₁₁ + x₁₂ + x₁₃ <= 18
x₂₁ + x₂₂ + x₂₃ <= 15
x₃₁ + x₃₂ + x₃₃ <= 23
x₄₁ + x₄₂ + x₄₃ <= 12

• Hay que respetar la capacidad en peso de cada compartimento:

x₁₁ + x₂₁ + x₃₁ + x₄₁ <= 10
x₁₂ + x₂₂ + x₃₂ + x₄₂ <= 16
x₁₃ + x₂₃ + x₃₃ + x₄₃ <= 8

• Hay que respetar la capacidad en volumen de cada compartimento:

480 x₁₁ + 650 x₂₁ + 580 x₃₁ + 390 x₄₁ <= 6800
480 x₁₂ + 650 x₂₂ + 580 x₃₂ + 390 x₄₂ <= 8700
480 x₁₃ + 650 x₂₃ + 580 x₃₃ + 390 x₄₃ <= 5300

• El peso de la carga en los tres compartimentos debe mantener la misma proporción que sus límites de capacidad de carga en peso:

(x₁₁ + x₂₁ + x₃₁ + x₄₁)/10 =

= (x₁₂ + x₂₂ + x₃₂ + x₄₂)/16 =

= (x₁₃ + x₂₃ + x₃₃ + x₄₃)/8

• El objetivo es maximizar el valor total de la carga:

maximizar 310 (x₁₁+ x₁₂+ x₁₃) +

+ 380 (x₂₁+ x₂₂+ x₂₃) +

+ 350 (x₃₁+ x₃₂+ x₃₃) +

+ 285 (x₄₁+ x₄₂+ x₄₃)

En esta asignatura veremos cómo resolver este tipo de problemas para, en el caso que nos ocupa, llegar a obtener la siguiente solución óptima (calculada con esta herramienta en línea) (nueva versión):

x₁₁ = 0, x₁₂ = 0, x₁₃ = 0, x₂₁ = 7, x₂₂ = 0, x₂₃ = 8, x₃₁ = 3, x₃₂ = 12.9474, x₃₃ = 0, x₄₁ = 0, x₄₂ = 3.05263, x₄₃ = 0

Valor total óptimo de la carga: 12151.6 €

Veamos qué se le ocurrió a Alice para ganar a Bob siempre que fuera posible (en el juego que quedó pendiente en julio).

Al principio hemos considerado un juego con dos montones de 10 piedras cada uno, denominaremos ese juego como 10+10 y a un montón le llamaremos A y al otro B. De esta manera, n+m es un juego en el que el montón A tiene n piedras y el montón B tiene m piedras.

Alice rellenó poco a poco, y empezando por los valores bajos de n y m, una tabla como la que se incluye arriba, en la que las filas corresponden al montón A y las columnas al montón B. Cada casilla de la tabla contiene un símbolo que puede ser una flecha o un asterisco. La flecha indica la casilla a la que Alice debe moverse para mantener intactas sus opciones de victoria. Por ejemplo, la flecha ← de la casilla (2,3) indica que tiene que retirar una piedra del montón B. Un asterisco en (i,j) quiere decir que, si Bob también sabe jugar así de bien, no hay opción de ganarle en el juego i+j…

Como Bob no podía soportar más esta situación, optó finalmente por matricularse en Algoritmia Básica.

Fuente: An Introduction to Bioinformatics Algorithms, Neil C. Jones y Pavel A. Pevzner. The MIT Press, 2004.

Bob y Alice se aburren un sábado por la tarde. Como sólo disponen de 20 piedras para entretenerse, deciden agrupar las piedras en dos montones de 10 y jugar al siguiente juego:

1. En cada turno, un jugador puede coger una piedra de un montón o una piedra de ambos montones.
2. Una vez cogidas, las piedras son retiradas del juego.
3. Gana el jugador que coge la última piedra.
4. Empieza Alice.

En un principio, no está claro cuál es la estrategia ganadora, o incluso si existe una. ¿Tiene el primer jugador o el segundo siempre ventaja? Bob intenta analizar el juego y rápidamente se da cuenta de que existen demasiadas variantes en un juego con 10 piedras en cada montón. Así que intenta diseñar una estrategia para un juego con 2 piedras por montón, de esta manera obtiene la siguiente “receta ganadora”:

Si Alice coge una piedra de ambos montones, yo cogeré las piedras sobrantes (una de cada montón) y ganaré. Si Alice coge sólo una piedra, yo cogeré la otra piedra del mismo montón. Así la única opción de Alice será coger una piedra del otro montón, yo podré coger la que queda y ganaré.

Entusiasmado con esta estrategia, Bob, generaliza de manera directa su estrategia para un juego de n piedras por montón, y haciendo un acto de fe, asume que el segundo jugador siempre puede ganar si n >= 2. Sin embargo, no siempre gana.

Por su parte Alice, que ha cursado Algoritmia Básica, diseña una estrategia general y fácil de aplicar que le asegura la victoria para ciertos valores de n.

¿Sabrías decir cuáles son esos valores? ¿En qué consiste la estrategia?

Fuente: Se publicará más adelante…

Volvemos en septiembre, os deseamos buen verano.

Bob y Alice

La algoritmia tiene aplicaciones en multitud de campos de la Ingeniería, la Ciencia, el Arte… también en la Botánica.

En la Universidad de Calgary (Canadá), trabaja un grupo de investigación en “Botánica algorítmica”, dirigido por el Profesor Przemyslaw Prusinkiewicz. En su página web (en este enlace) puede encontrarse abundante material sobre los trabajos del grupo.

Armonía en verde.

Este sosegado lugar, reminiscencia del cuadro de 1899 de Claude Monet “Armonía en verde”, de su ciclo de pinturas al óleo “Los nenúfares”, en realidad, no existe. La escena se ha realizado utilizando L-sistemas ["L" por Lindenmayer, autor de una teoría desarrollada para modelar el crecimiento de las plantas] que capturan el crecimiento de árboles y plantas acuáticas, e iluminada mediante simulación de la luz solar. Es difícil no apreciar hasta qué punto la teoría de los L-sistemas y todo el campo de la informática gráfica, se han desarrollado desde sus inicios en la década de 1960, haciendo posibles estas imágenes.  Sin embargo, los resultados obtenidos hasta la fecha no son concluyentes y constituyen sólo una introducción a la investigación sobre la modelización de plantas con fines biológicos y gráficos. La belleza algorítmica de las plantas está abierta a más exploración.

(Fuente: The Algorithmic Beauty of Plants, P. Prusinkiewicz y A. Lindenmayer, 2004, versión electrónica disponible en http://algorithmicbotany.org/papers/#abop)

Inflorescencia de lilas.

     n=10, δ = 60º

     #include K /* flower shape specification */
     ω  : A~K
     p1 : A    :  *      → [-/~K][+/~K]I(0)/(90)A
     p2 : I(t) :  !(t=2) → FI(t+1)
     p3 : I(t) :  t=2    → I(t+1)[-FFA][+FFA]

La regla p1 describe el crecimiento subapical de un eje. La regla p2 modela la elongación lineal de internodos en el tiempo e introduce un retraso antes de que p3 cree el eje lateral. La rotación del ápice en 90º (p1) da lugar a un patrón de ramificación decusado con pares consecutivos de ejes de orden (n+1) colocados en los planos que pasan por el eje de orden n y son perpendiculares entre sí.

(Fuente: The Algorithmic Beauty of Plants, P. Prusinkiewicz y A. Lindenmayer, 2004, versión electrónica disponible en http://algorithmicbotany.org/papers/#abop)