[Iremos publicando noticias. Para recibirlas, puedes añadir este enlace: "RSS de las entradas" en tu agregador de noticias o bien seguirnos en Twitter.]

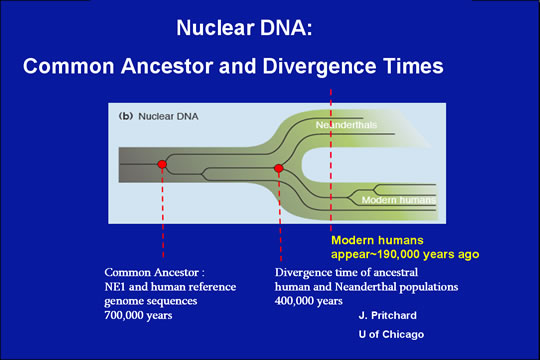
Hace 150 años se encontraron por vez primera partes del esqueleto del denominado hombre de Neandertal cerca de Düsseldorf (Alemania). Desde entonces, hemos querido saber qué relación existe entre el Homo sapiens, nuestro antepasado, y el de Neandertal.

Hoy sabemos que el Homo neanderthalensis no es un ancestro del Homo sapiens, y viceversa. Las diferencias encontradas entre el genotipo del Homo sapiens y el del Homo neanderthalensis lo demostraron. Las nuevas tecnologías nos permiten extraer genotipos de huesos de más de 30000 años de antigüedad. Los genotipos se extraen en forma de secuencias de ADN. Estas secuencias son como los planos de construcción de los seres vivos. Con el transcurso del tiempo, las secuencias de ADN cambian debido a mutaciones. Dadas las secuencias de ADN de diferentes especies, se puede calcular su similitud con la ayuda de un computador. Medimos la similitud de dos secuencias mediante la especificación de la distancia entre ellas. Una pequeña distancia entre dos secuencias de ADN indica una gran similitud entre ambas. Pero, ¿cómo se calcula la distancia entre dos secuencias de ADN? En esta asignatura veremos cómo se diseña un algoritmo para resolver este problema. Para ello, necesitaremos un modelo matemático de las secuencias de ADN, de las mutaciones, y de la distancia entre dos secuencias.

Una secuencia de ADN se compone de bases. Una secuencia de tres bases codifica un aminoácido. Existen cuatro bases diferentes, que suelen representarse con las letras A, G, C y T. Por tanto, una secuencia de ADN puede representarse con una cadena de símbolos del alfabeto Σ = {A, G, C, T}.

Por ejemplo, CAGCGGAAGGTCACGGCCGGGCCTAGCGCCTCAGGGGTG, es una parte de la secuencia de ADN de un pollo.

En la naturaleza, las secuencias de ADN cambian a causa de las mutaciones. Una mutación puede considerarse como una aplicación desde una secuencia de ADN x a otra secuencia de ADN y. Supongamos que todas las mutaciones se pueden modelar utilizando los siguientes tres tipos básicos de mutaciones:

1. borrado de un carácter,
2. inserción de un carácter, y
3. sustitución de un carácter por otro carácter.

Por ejemplo, sea x = AGCT una secuencia de ADN. Entonces, la mutación “sustituir G por C” mutaría x a la secuencia y = ACCT. Utilizamos la notación “a → b” para representar la sustitución de a por b. De igual forma, “a →” representa el borrado del carácter a, y  “→ b” es la inserción del carácter b. Además, debe especificarse explícitamente la posición en la que se produce la mutación.

Para medir la distancia entre dos secuencias de ADN, damos un coste específico a cada mutación básica. La mutación s tiene coste c(s). El coste de una mutación se corresponde con la probabilidad de esa mutación. Cuanto más probable sea una mutación, más bajo será su coste. Utilizamos los siguientes costes para las tres mutaciones básicas:

• borrado: 2
• inserción: 2
• sustitución: 3

Para comparar dos secuencias de ADN x e y, se requiere en la mayoría de los casos más de una mutación básica transformando x en y. Por ejemplo, si queremos comparar x = AG con y = T, entonces no sería suficiente con una mutación básica.

Pero podríamos obtener la transformación usando la secuencia de mutaciones S = A →, G → T (es decir, borrar A y luego sustituir G por T). El coste c(S) de una secuencia de mutaciones, S = s₁. . . , s_t es la suma de los costes de sus mutaciones básicas, es decir,

c(S) := c(s₁) + … + c(s_t).

La distancia entre dos secuencias de ADN se define como el coste de una secuencia específica de mutaciones que transforma una en la otra. El problema es que puede haber muchas secuencias diferentes de mutaciones que transforman una secuencia de ADN en otra. Por ejemplo, podríamos utilizar las siguientes secuencias de mutaciones para transformar la secuencia x = AG en y = T:

• S₁ = A →, G → T;
  c(S₁) = c(A →) + c(G → T) = 2 + 3 = 5
• S₂ = A → T, G →;
  c(S₂) = c(A → T) + c(G →) = 3 + 2 = 5
• S₃ = A →, G →, → T;
  c(S₃) = c(A →) + c(G →) + c (→ T) = 2 + 2 + 2 = 6
• S₄ = A → C, G →, C →, → T;
  c(S₄) = c(A → C) + c(G →) + c(C →) + c(→ T) = 3 + 2 + 2 + 2 = 9

Existen muchas otras secuencias que transforman x en y, pero ninguna de ellas tiene un coste menor que el de las secuencias S₁ y S₂. Para definir la distancia entre dos secuencias de ADN, usamos la secuencia de mutaciones de menor coste. Dada una función de coste c, la distancia de d_c(x,y) de las secuencias de ADN x e y se define como

d_c(x,y) := min{ c(S) | S transforma x en y }.

Por ejemplo, las secuencias S₁ y S₂ son las secuencias de mutaciones con mínimo coste que transforman x = AG en y = T. Por tanto, la distancia evolutiva d_c(x,y) entre x e y es 5.

El cálculo de la distancia evolutiva entre dos secuencias de ADN es uno de los problemas que estudiaremos en esta asignatura.

Fuente: Algorithms Unplugged, B. Vöcking, H. Alt, M. Dietzfelbinger, R. Reischuk, C. Scheideler, H. Vollmer, D. Wagner (eds.), Springer, 2011.