Para ganar a ‘Piedra, papel o tijera’, hace falta conocer bien la psicología de tu adversario:

o hacer algo de trampa:

En cualquier otro caso, no será posible diseñar una estrategia ganadora. Formalicemos un poco el juego: Mediante matrices se pueden representar diversos juegos como el que inventaron Bob y Alice (ver entrada) o como ‘Piedra, papel o tijera’. Supongamos que dos jugadores, llamados Row y Column, deciden jugar a ‘Piedra, papel o tijera’. La ganancia del jugador Row (y equivalentemente la pérdida del jugador Column) puede representarse con la siguiente matriz.

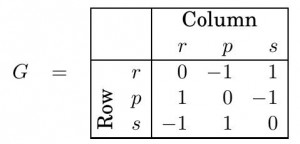
Las letras ‘r’, ‘p’ y ‘s’, se corresponden con las jugadas piedra (rock), papel (paper), tijera (scissors). Así, la entrada 1 de la fila ‘p’ y columna ‘r’ indica que si Row elige papel y Column piedra, entonces Row gana un punto.

¿Existe alguna estrategia ganadora para este juego? Es decir, ¿puede alguno de los jugadores asegurarse la victoria a la larga si juega óptimamente? Obviamente, si Row siempre elige la misma jugada, por ejemplo piedra, Column se percatará de su inocente estrategia, acabará sacando siempre papel y ganándole. Conviene por tanto despistar lo máximo posible al oponente eligiendo las jugadas de manera aleatoria. En clase confirmaremos el pensamiento intuitivo que nos dice que si los dos juegan lo mejor posible, es decir maximimizan el valor esperado de su ganancia (en este caso eligiendo al azar entre las tres jugadas), a la larga terminarán en empate. Lo mismo ocurrirá si introducimos dos jugadas más, ‘lagarto’ y ‘Spock’:

Imagina ahora que se obliga a Row a anunciar públicamente su estrategia (es decir la probabilidad con que elegirá piedra, papel y tijera) y Column puede elegir la suya en función de la de Row. ¿Se verá Row perjudicado por esta nueva regla del juego?

Y, ¿qué pasaría si en vez de ‘Piedra, papel o tijera’ o ‘Piedra, papel, tijera, lagarto o Spock’ , consideráramos un juego con la siguiente matriz?

¿Existe ahora una estrategia ganadora para alguno de los jugadores?

Trataremos este tipo de juegos en clase y veremos que se pueden obtener respuestas a estas preguntas mediante programación lineal.