Cada nodo izquierdo de la figura representa a un chico y cada nodo derecho una chica. Hay un arco conectando dos personas si existe atracción mutua. Por ejemplo a Al le gustan todas las chicas y Al gusta a todas las chicas. ¿Es posible emparejar a todos de tal manera que todos estén contentos con su pareja? Es decir ¿existe el emparejamiento perfecto (perfect matching)?

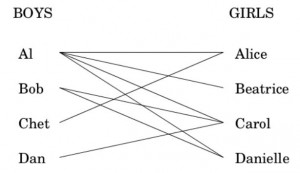
Este problema puede “transformarse”, en otras palabras “reducirse”, a un problema de flujo máximo en una red. El problema de flujo máximo consiste en calcular cuál es flujo máximo que puede producir un nodo fuente y alcanzar el nodo sumidero sin violar las capacidades de los arcos de la red. En las clases de Algoritmia Básica veremos que este problema puede resolverse de manera eficiente mediante un problema de programación lineal. La reducción del problema del emparejamiento perfecto es sencilla: simplemente hay que transformar el grafo inicial por uno similar con un nodo fuente “s” y un nodo sumidero “t”, dirigir todos los arcos en la dirección de las chicas y asignar una capacidad de uno a todos los arcos.

Habrá un emparejamiento perfecto si y sólo si el flujo máximo es igual al número de parejas deseado, es decir, en nuestro caso igual a 4. ¿Puedes encontrar ese emparejamiento?  o ¿siempre habrá alguien descontento?

Fuente: Algorithms, S. Dasgupta, C. H. Papadimitriou, U. V. Vazirani. Mc Graw-Hill, 2008.