Listas con Punto de Interés

Estructuras de Datos LinealesListas con Punto de Interés
Descripción informal Especificación Implementación por medio de dos pilas Implementación secuencial Implementación encadenada Descripción informal Las estructuras lineales pila y cola tienen la limitación de que la inserción, consulta y borrado de los elementos se realiza únicamente por sus extremos, pero en ocasiones puede interesar realizar dichas operaciones sobre cualquier elemento de la secuencia. Para poder trabajar sobre un punto cualquiera de la secuencia se define el tipo lista con punto de interés. La idea es tener, junto a la secuencia de elementos, un apuntador a la posición de dicha secuencia en la que se trabaja. Se dispondrá de operaciones para insertar, borrar y consultar respecto a dicho punto, y se ha de disponer de otras operaciones para moverlo. El modelo es semejante a un terminal en donde el cursor indica la posición en que se realizarán las operaciones de modificación de la secuencia, y donde se dispone de funciones para desplazar dicho cursor. En las secuencias se distinguirá entre la subsecuencia que se encuentra a la izquierda del punto de interés (p.d.i.) y la subsecuencia que empieza a partir de éste. 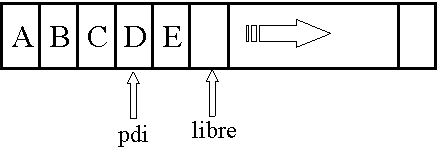Por tanto definiremos la lista como: l =<s, t> Î V* x V* s=s₀ s₁ … s_n " i,j 0<= i <= n 0<= j <= m s_i, t_jÎV t= t₀t₁ … t_m Por ejemplo la lista A B C D E, con el punto de interés sobre la D, la representaremos como < A B C , D E > A partir de este modelo, y suponiendo la siguiente lista l = < s₀ s₁ … s_n , t₀ t₁… t_m> se puede estudiar cómo se comportarán las diferentes operaciones necesarias para trabajar con listas con p.d.i. Crear la lista vacía: genera una secuencia con dos subsecuencias vacías, en donde el punto de interés se encuentra al final del todo < l , l > Insertar el elemento e: < s₀ … s_ne , t₀ … t_m > Por ejemplo, si insertamos el elemento F en la lista A B C D E donde el elemento D está bajo el punto de interés nos quedará la lista A B C F D E Borrar: borra el elemento bajo el punto de interés < s₀ … s_n, t₁ … t_m > Si el punto de interés se encuentra a la derecha del todo, aplicar la operación de borrar producirá un error. A B C D E ==> A B C D ==> error Consultar: Devolverá el elemento t₀ A B C D E ==> D Ir al principio: desplaza el pdi al principio de la secuencia < l, s₀ … s_n t₀ … t_m > A B C D E ==> A B C D E Avanzar: < s₀ … s_nt₀ , t₁ … t_m > A B C D E == A B C D E ¿Final?: comprueba si la lista es de la forma < s₀ … s_n t₀ … t_m , l > A B C D E _ ¿Lista Vacía?: comprueba si la lista está formada por dos subsecuencias vacías. < l , l > Especificación A continuación se muestra la especificación formal de las listas con Punto de Interés Especificación lista_con_pdi (elemento) usa booleano tipo lista operaciones crear: -> lista insertar: lista x elemento -> lista borrar: lista -> lista principio: lista -> lista avanzar: lista -> lista actual: lista -> elemento final: lista -> booleano vacía: lista -> booleano privada listar: sec x sec -> lista privada secvacia: -> sec privada ins: sec x elemento -> sec errores "s Î sec borrar (listar(s, secvacia)) avanzar (listar(s, secvacia)) actual (listar(s, secvacia)) ecuaciones "s, s' Î sec, " e Î elemento crear = listar (secvacia, secvacia) insertar (listar(s , s'), e) = listar(ins(s,e), s') borrar (listar(s, ins(s', e))) = listar(s , s') principio (listar(secvacia, s)) = listar( secvacia, s) principio(listar(ins(s , e), s')) = principio(listar(s, ins (s',e))) avanzar (listar(s, ins(s', e))) = listar( ins (s, e), s') actual (listar(s, ins (s', e))) = e final (listar(s, secvacia)) = cierto final (listar(s, ins(s', e))) = falso vacía (listar (secvacia, secvacia) = cierto vacía (listar (s, ins(s', e)) = falso vacía (listar (ins(s', e), s) = falso Fespecificación Implementación por medio de dos pilas Sabiendo que se pueden realizar las diferentes operaciones sobre pilas con un coste Q(1), se puede ver fácilmente que el coste de las operaciones sobre listas con pdi es: crear Q (1) insertar Q (1) borrar Q (1) principio Q (n) avanzar Q (1) actual Q (1) final Q (1) vacía Q (1) Siendo un inconveniente el coste lineal de la operación de ir al principio. A nivel espacial, el coste también es Q(n) pudiéndose implementar sobre una sola tabla que contenga las dos pilas. 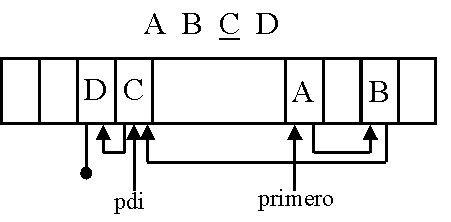Implementación secuencial: Consiste en representar la secuencia dentro de un vector ordenada de acuerdo a su posición en la lista, utilizándose dos apuntadores para indicar la posición del pdi y la primera posición libre. A modo de ejemplo se presenta su posible implementación y un par de funciones del TAD: elems = = tabla [1..MAX] de elemento lista = = tupla vector: elems libre, pdi: entero ftupla función crear retorna lista var l: lista fvar l.libre := 1 l.pdi := 1 retorna l ffuncion función insertar (ent l: lista, ent e: elemento) retorna lista var i: entero fvar si l.libre > MAX entonces Tratamiento_de_Error sino i := l.libre mientras i > l.pdi hacer l.vector[i] := l.vector[i-1] i := i - 1 fmientras l.libre := l.libre +1 l.vector[l.pdi] := e l.pdi := l.pdi +1 fsi retorna l ffuncion El coste de las operaciones de acuerdo a este modelo sería: crear Q (1) insertar Q (n) borrar Q (n) principio Q (1) avanzar Q (1) actual Q (1) final Q (1) vacía Q (1) El coste de dos operaciones muy elementales, como son insertar y borrar, es de Q(n), siendo el coste espacial nuevamente Q(n). Por tanto no es una buena solución. Implementación encadenada Se desea evitar costes lineales en las operaciones más básicas sobre listas. Para ello no se puede tener los elementos de la lista ordenados secuencialmente. En su lugar se encadenará cada elemento con el siguiente, por medio de apuntadores. nodo = = tupla e: elemento enc: entero ftupla nodos = = tabla [1..MAX] de nodo lista = tupla vector: nodos pdi, primero: entero ftupla Esta implementación tiene el problema de la necesidad que gestionar el espacio libre en las inserciones y borrados. Se puede pensar en dos posibles soluciones: Añadir una marca de posición libre a cada elemento, lo que implicaría un coste Q(n) en la inserción. Utilizar una pila de posiciones libres, utilizando el mismo campo de encadenamiento Esta opción tiene el problema de que para borrar o insertar elementos se debe acceder al elemento anterior al pdi, lo que conlleva un coste Q(n) para recorrer la tabla en su búsqueda. 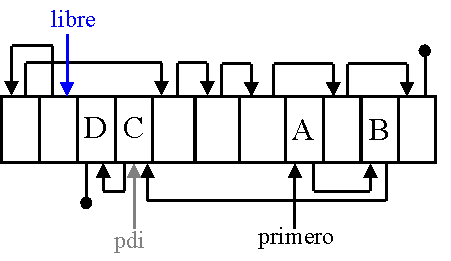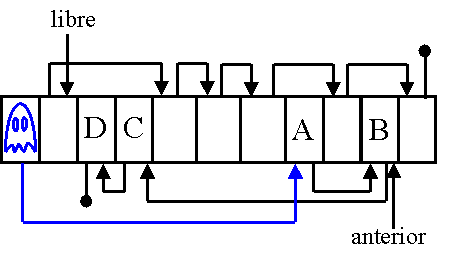Una solución es tener una lista de doble encadenamiento, pero ello implica necesitar el doble de espacio para apuntadores. Otra solución, que será la que se adopte, es apuntar no al pdi sino al elemento anterior al pdi, de modo que en coste lineal, siguiendo el encadenamiento del elemento apuntado, se accede al pdi. Esta última solución nos genera el problema de dónde apuntar cuando el pdi está al principio de la lista, que se resuelve creando un elemento fantasma, el cual puede situarse siempre al principio de la lista, de modo que no haga falta tener un apuntador al inicio de la lista. Los costes de las operaciones sobre listas con pdi, con implementación encadenada por apuntadores son los siguientes: crear Q (n) insertar Q (1) borrar Q (1) principio Q (1) avanzar Q (1) actual Q (1) final Q (1) vacía Q (1) Puede verse que los costes en las operaciones más críticas es de Q(1), y la única operación con coste Q(n) es la de crear, que al ejecutarse una sola vez al principio de todo no es muy tan importante. Por otro lado el coste espacial sigue siendo Q(n). Ambos costes podrán evitarse con la implementación en memoria dinámica encadenada por punteros.

Autoría Correo de contacto Fecha de actualización