Tamaño total = 500.000 * 512 bytes = 256Mbytes.

 -> demasiado grande para guardarlo en memorial principal.

 -> necesitamos guardarlo en disco (memoria externa).

Un bloque de disco es, por ejemplo,  8.192 bytes.
Por tanto, el número de bloques que necesitamos es  =
        256Mbytes / 8.192 bytes por bloque  = 31.250 bloques.

Cada bloque guarda 16 registros.

A grosso modo tenemos (si usamos un bloque de disco en cada nodo de un árbol):

  => 15 niveles en un árbol binario con 16 registros por nodo.

Cada acceso a disco:

  tiempo acceso = tiempo búsqueda + rotational delay + tiempo transferencia de bloque
                = 70 milésimas de segundo (aprox.)

tiempo de búsqueda (caso peor)  = 15 * 70 ms = 1 segundo.

El acceso a disco es aproximadamente 10.000 veces más lento que la memoria principal.

Desgraciadamente todavía es peor si miramos el coste de inserción o borrado...

Pregunta: ¿Existe  alguna forma de tener búsqueda, inserción y borrado rápidos teniendo los datos en disco?

Respuesta:

Sí

Usando una estructura similar a los árboles 2-3-4 pero con muchos más datos por nodo:

         -> árbol B.

Un árbol B de orden M tiene las siguientes propiedades :
 

Considera T, un árbol B de orden M.

Si T contiene un total de N datos y P nodos, entonces cada nodo contiene al menos M/2-1 datos

        P<= N/(M/2-1)+1

        P >= 1 + 2 + 2(M/2) + 2(M/2)^2 + 2(M/2)^3 + ... + 2(M/2)^H

          = 1+2((M/2)^{H+1} - 1)/(M/2 - 1))

        H <= log_(M/2) (N + 1)  - 1

        H <= log_8 (500.001) - 1 
          = 5,3

Esto nos da un tiempo de acceso a disco de sólo  6 * 70ms = 420ms. (menos de la mitad que antes)

Un árbol binario equilibrado con un dato por nodo necesita 
    log_2 500.001 - 1 = 17,9 niveles.

Por tanto para disminuir la altura necesitamos:

• árboles de grado alto
• mantener los nodos lo más llenos posible (al menos al 50%).

Objetivo: Hacer subdivisiones de nodos que requieran la menor interacción posible entre nodos adyacentes (y por tanto acceso a disco mínimo).

Ejemplo de inserción en un árbol B

Consideremos la inserción de los siguientes datos en un árbol B de orden 5:

20, 40, 60, 80, 70, 10, 30, 15, 75, 85, 90, 25, 35, 50, 22, 27, 32

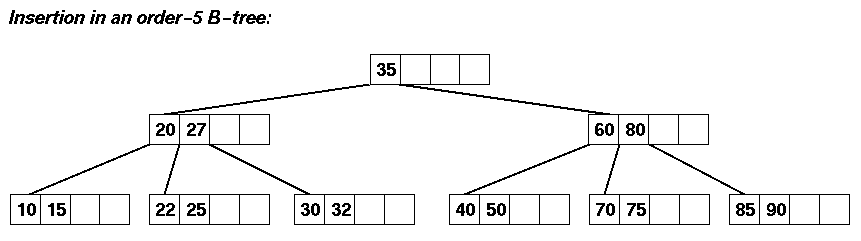
Notemos que ningún nodo (excepto la raiz) está nunca menos del 50% lleno. Tenemos que mantener los nodos bastante llenos, pero no demasiado para evitar demasiadas subdivisiones.
 

Eficiencia de un árbol B

Usando el ejemplo de la guía telefónica, si tenemos un árbol B con nodos que están al menos medio llenos entonces la altura es aproximadamente 5,3

Los punteros a los hijos se guardan en el nodo, reduciendo un poco la cantidad de datos que se pueden guardar en cada nodo.

Para insertar sin subdivisiones de nodos, necesitamos 6 accesos a disco para buscar el nodo, más un acceso a disco para escribir el nodo actualizado. Total 7 accesos a disco

Para insertar con una subdivisión de nodo, necesitamos 5 accesos más a disco (más los 6 de búsqueda), total 11 accesos a disco.