• Después de insertar un nodo en el subárbol derecho del hijo derecho.
• Después de insertar un nodo en el subárbol izquierdo del hijo derecho.

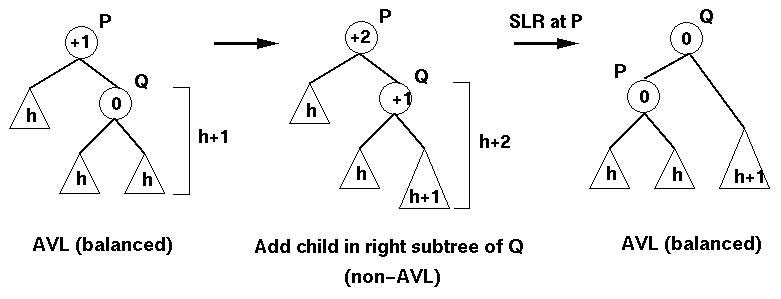
Inserción de un nodo en el subárbol derecho del hijo derecho:

Esto implica una rotSI(P):

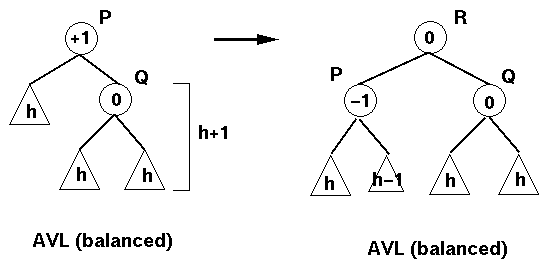
Inserción de un nodo en el subárbol izquierdo del hijo derecho:

Esto implica una rotDD(P):

En ambos casos el árbol es reequilibrado localmente.

Inserción requiere:

• búsqueda del punto de inserción (tiempo O(altura))
• actualizar los factores de equilibro en el camino desde el punto de inserción hacia la raiz, pero sólo hasta encontrar un 2 ó -2 (si no aparecen hasta la raiz)  (tiempo O(altura))
• reequilibrado (si es necesario), es decir, una rotación (tiempo O(1))

En el 53% de los casos no hace falta reequilibrado.
Ejemplo: Dado el siguiente árbol AVL, insertar el nodo con valor 9:
                        6

                      /   \

                     3     12

                      \    / \

                       4  7   13

                           \

                            10