Introducción a los árboles de búsqueda equilibrados
- Recorrido inorden seguido de reconstrucción a partir del véctor ordenado
- El algoritmo DSW (C. Day, Q. Stout y B. Warren).
- búsqueda en árbol equilibrado: O(log N), pero
- inserción y reequilibrado: O(N).
- La idea es definir una clase de BST que sean casi equilibrados y usar una técnica de reequilibrado local.
- En este caso se puede demostrar que podemos tener tiempos de inserción y búsqueda O(log N).
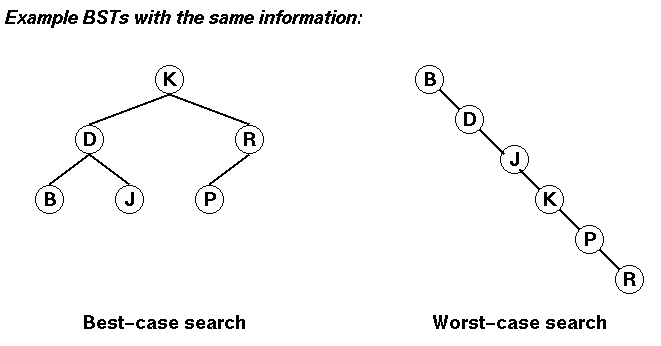
Sabemos que el tiempo de búsqueda en árboles binarios de búsqueda depende de la altura del árbol. El árbol puede llegar a tener altura máxima O(N).
Podríamos disminuir ese tiempo si mantuviéramos árboles de altura mínima (completos o casi-completos).
En ese caso el tiempo de búsqueda sería
O(log N).
Idea:
Mantener el BST lo más equilibrado posible reequilibrándolo
cada vez que insertemos, utilizando algoritmos de reequilibrado globales.
Ejemplo de algoritmos de reequilibrado de BST:
El coste de los algoritmos de reequilibrado puede ser O(N)
Así que tenemos:

Pregunta:
¿Hay forma de alcanzar búsqueda en tiempo O(log N) y a la vez inserción en tiempo O(log N)?
Respuesta:
SI 
Un método clásico para hacer esto es
usar un árbol AVL (Adelson-Velskii y Landis).
elvira at posta.unizar.es
karmelo at posta.unizar.es
Fecha de actualización: 5-9-01
