Borrado en arboles binarios de búsqueda
- Caso 1: El nodo a borrar no tiene hijos (es una hoja)
- Caso 2: El nodo a borrar tiene hijo izquierdo pero no tiene hijo derecho
- Caso 3: El nodo a borrar tiene hijo derecho pero no tiene hijo izquierdo
- Caso 4: El nodo tiene dos hijos
- Seleccionar el nodo de más a la dcha en el subárbol izdo
- Desligar este nodo del árbol, conectar su subárbol izdo al padre
- Conectar el nodo desligado en el nodo borrado
Queremos borrar el nodo que contiene un determinado elemento en un BST
Hay que encontrar el nodo y examinar cuatro posibles casos:
Caso 1: El nodo a borrar no tiene hijos
Inmediato:
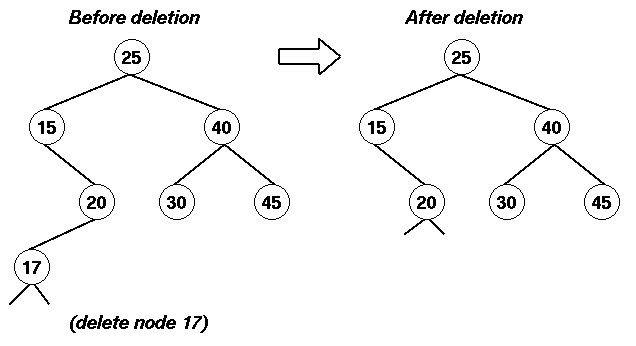
Caso 2: El nodo a borrar tiene hijo izquierdo pero no tiene hijo derecho
Aquí, el subárbol hijo izdo se une al padre del nodo a borrar
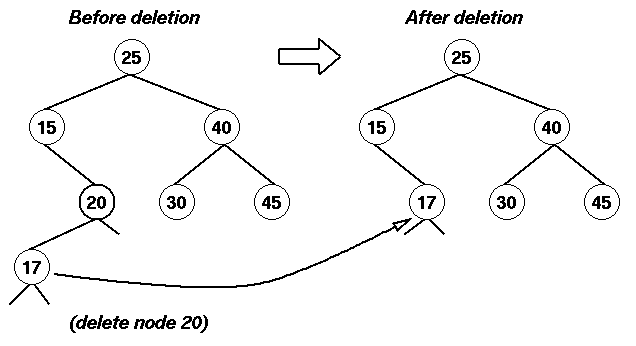
Caso 3: El nodo a borrar tiene hijo derecho pero no tiene hijo izquierdo
Aquí, el subárbol hijo dcho se une al padre
del nodo a borrar
.
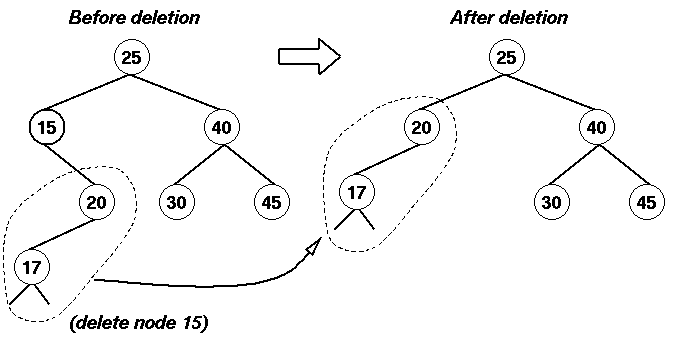
Caso 4: El nodo tiene dos hijos
Un nodo con dos hijos tiene elementos en sus subárboles que son mayores y menores que él mismo. Hay que preservar el orden correcto.
Hay dos subcasos:
El hijo izdo tiene un hijo dcho:
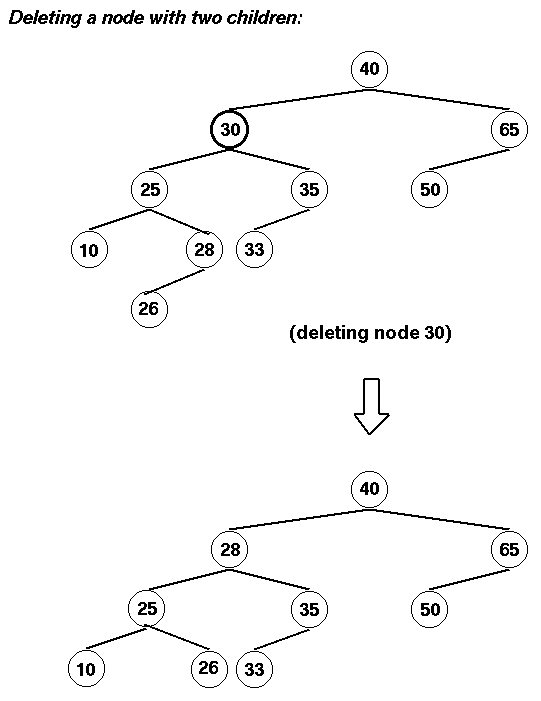
En este ejemplo el hijo izdo (25) del nodo borrado tiene un hijo dcho (28):
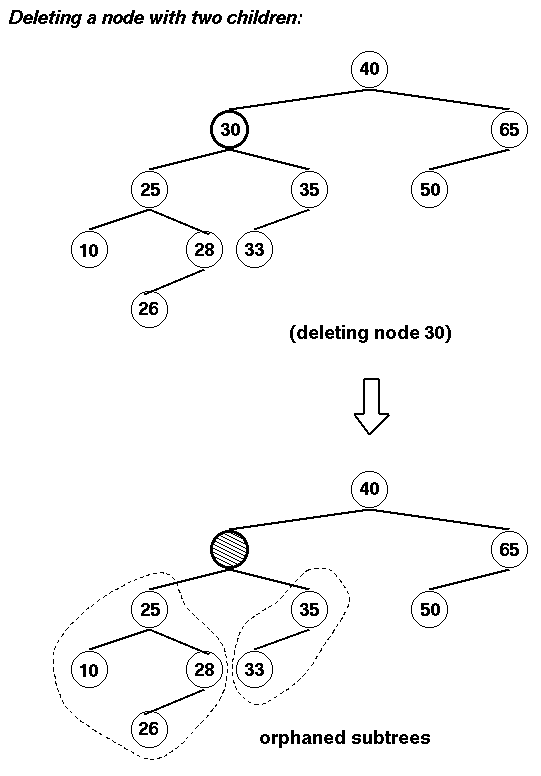
Aquí el algoritmo es:
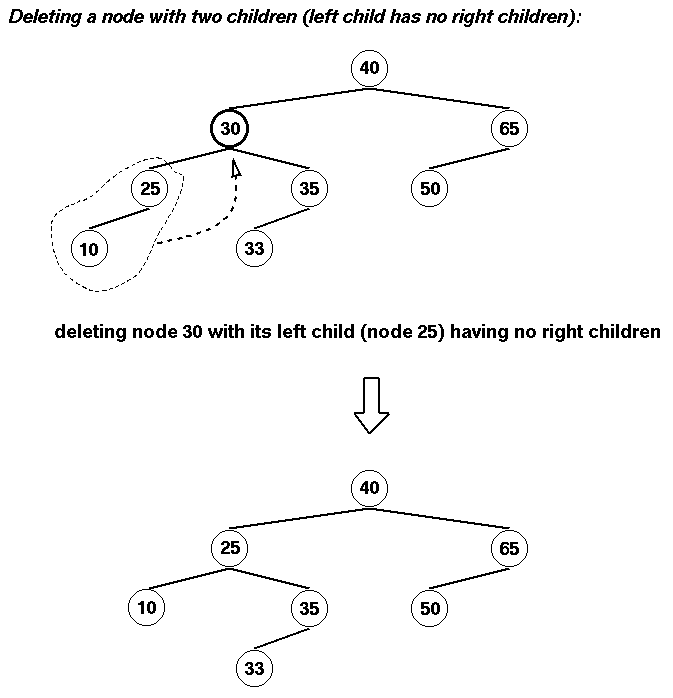
El hijo izdo no tiene hijo dcho:
Este es un caso más simple ya que el mayor nodo del subárbol izdo es el hijo izdo.
La operación simplemente es conectar el hijo izdo
al nodo borrado y hacer que el hijo dcho del nodo borrado sea su hijo dcho.
¿Hemos mejorado con los BST?
elvira at posta.unizar.es
karmelo at posta.unizar.es
Fecha de actualización: 5-9-01
