DeLorean
DeLorean (DEscription LOgic REasoner with vAgueNess) is a fuzzy rough Description Logic (DL) reasoner. It supports fuzzy rough extensions of the fuzzy DLs SROIQ(D) and SHOIN(D), which are equivalent to the ontology languages OWL and OWL 2, under finite Gödel, finite Łukasiewicz and Zadeh fuzzy logics.
Given a fuzzy rough ontology in our fuzzy rough extension of OWL or OWL 2, DeLorean computes an equivalent non-fuzzy representation in OWL or OWL 2, respectively.
In a strict sense, DeLorean is not a reasoner but a translator from a fuzzy rough ontology language into apublic classical ontology language (OWL or OWL 2). Then, apublic classical DL reasoner is employed to reason with the resulting ontology. But due to this ability of combining the reduction procedure with the crisp reasoning, we refer to DeLorean as a reasoner.
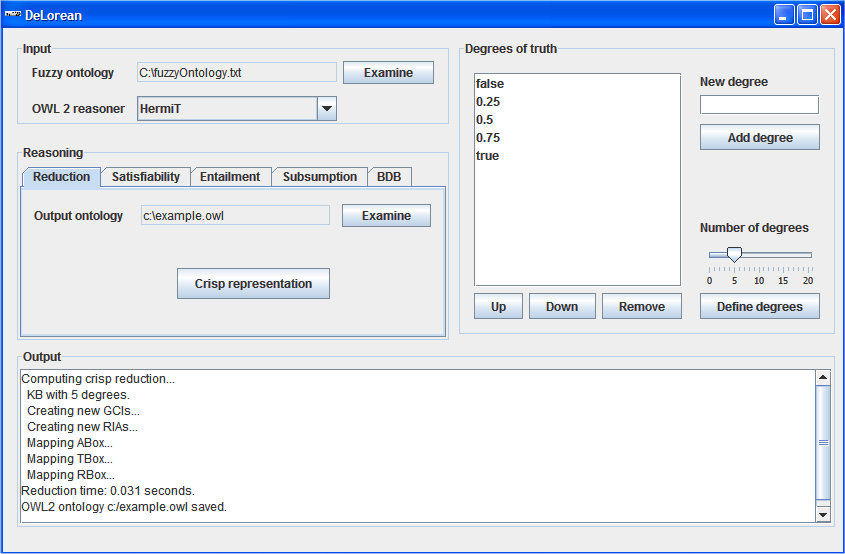
The inputs of the system are the path of the fuzzy rough ontology, the path of the output non-fuzzy ontology and the reasoner. The reasoner can be Pellet, or the URL of any DIG-complaint DL reasoner. The outputs of the system are the result of the consistency test, the reduction time and the reasoning time. Of course, some error messages are shown if necessary.
DeLorean can also be used as a stand-alone application but also as an API from Java applications.
Related publications
F. Bobillo, M. Delgado, J. Gómez-Romero. DeLorean: A Reasoner for Fuzzy OWL 2. Expert Systems with Applications 39(1):258-272, 2012.- F. Bobillo. Managing Vagueness in Ontologies. PhD Dissertation, University of Granada, Spain, December 2008.
Complete list of publications from the developer.
Syntax
The language assumes three alphabets of symbols, for individuals, concepts (fuzzy sets of individuals), and roles (fuzzy binary relation between individuals).
The axioms of a fuzzy knowledge base are grouped in three parts: a fuzzy ABox (axioms about individuals), a fuzzy TBox (axioms about concepts), and a fuzzy RBox (axioms about roles).
Notation
- We assume a finite chain of degrees of truth T = {x0 < x1 < x2 < ... < xP}, where x0 = true (= 0), xP = true (= 1), and xi is a String (possibly representing a numerical value)
- C is a fuzzy concept
- a,b are individuals
- R is a fuzzy role
- S is simple fuzzy role
- s is a fuzzy similarity relation (reflexive and symmetric)
- M is a strictly positive natural number
- N is a natural number
- d is a fuzzy datatype, defined with the syntax: (trapezoidal q1 q2 q3 q4)
- D is a degree in a finite chain T
- In fuzzy nominal concepts, d is in (x0,xP]. If omitted, xP is assumed
- If SIGN is >= or <, then d is in (x0,xP]
- If SIGN is > or <=, then d is in [x0,xP)
- SIGN is one of the following: >= (greater or equal), > (greater), <= (less or equal) or < (less). If SIGN D is omitted, >= xP is assumed
- SIGN+ is one of the following: >= (greater or equal) or > (greater) If SIGN+ D is omitted, >= xP is assumed
- The universal role *top-role* cannot appear in the RBox
Concept expressions
| A | Atomic concept |
| *top* | Top concept |
| *bottom* | Bottom concept |
| ([and | g-and | l-and z-and] C1 ... Cn) | (Gödel, Łukasiewicz and Zadeh) concept conjunction |
| (l-and C1 ... Cn) | Łukasiewicz concept conjunction |
| ([or | g-or | l-or | z-or] C1 ... Cn) | (Gödel, Łukasiewicz and Zadeh) concept disjunction |
| (l-or C1 ... Cn) | Łukasiewicz concept disjunction |
| ([not | l-not | z-not] C) | Łukasiewicz-Zadeh concept negation |
| (g-not C) | Gödel concept negation |
| ([some | g-some | z-some] R [C | d] ) | (Gödel and Zadeh) existential quantification |
| (l-some R [C | d] ) | (Łukasiewicz) existential quantification |
| (all | z-all R [C | d] ) | Zadeh universal quantification |
| (g-all R [C | d] ) | Gödel universal quantification |
| (l-all R [C | d] ) | Łukasiewicz universal quantification |
| (one-of a [D]) | Fuzzy nominal |
| (self S) | Local reflexivity |
| (cut C D) | Cut concept |
| (triangular t1 t2 t3 C) | Triangularly-modified concept |
| (at-least M S) | At-least min cardinality restriction |
| (g-at-most N S) | Gödel max cardinality restriction |
| (z-at-most N S) | Zadeh max cardinality restriction |
| (exactly N S) | Zadeh cardinality restriction) |
| (at-least M S [C | d] ) | At-least qualified min cardinality restriction |
| (g-at-most N S [C | d] ) | Gödel qualified max cardinality restriction |
| (z-at-most N S [C | d] ) | Zadeh qualified max cardinality restriction |
| (exactly N S [C | d] ) | Zadeh qualified cardinality restriction |
| (upper s C) | Upper fuzzy rough concept |
| (tight-upper s C) | Tight upper fuzzy rough concept |
| (loose upper s C) | Loose upper fuzzy rough concept |
| (lower s C) | Lower fuzzy rough concept |
| (tight-lower s C) | Tight lower fuzzy rough concept |
| (loose lower s C) | Loose lower fuzzy rough concept |
Role expressions
| R | Atomic role |
| *top-role* | Universal role |
A-Box
| (instance a C [SIGN D]) | a is instance of concept C with a degree SIGN D |
| (related a b R [SIGN D]) | a and b are related by R with a degree SIGN+ D |
| (g-not-related a b R [SIGN D]) | a and b are not (Gödel sense) related by R with a degree SIGN D |
| ([not-related | l-not-related | z-not-related] a b R [SIGN D]) | a and b are not (Zadeh-Łukasiewicz sense) related by R with a degree SIGN D |
| (same-as a b) | a and b represent the same individual |
| (different-to a b) | a and b should be interpreted as different individuals |
T-Box
| (g-implies-concept C1 C2 [SIGN+ D]) | Concept C2 subsumes (Gödel implication) concept C1 with a degree SIGN+ D |
| (kd-implies-concept C1 C2 [SIGN+ D]) | Concept C2 subsumes (Kleene-Dienes implication) concept C1 with a degree SIGN+ D |
| (l-implies-concept C1 C2 [SIGN+ D]) | Concept C2 subsumes (Łukasiewicz implication) concept C1 with a degree SIGN+ D |
| (equivalent-concepts C1 C2) | C1 is equivalent to C2 |
| (disjoint-concepts C1 .... Cn) | Concepts C1 ... Cn are mutually disjoint |
| (disjoint-union-concept C1 C2 .... Cn) | Equivalent to the pair of axioms (disjoint-concepts C2 .... Cn) and (equivalent-concepts C1 (or C2 ... Cn)) |
| (crisp-concept C) | C is crisp |
R-Box
| (g-implies-role R1 R2 ... Rn R [SIGN+ D]) | Role R subsumes (Gödel implication) the role chain R1 ... Rn with a degree SIGN+ D |
| (kd-implies-role R1 R2 ... Rn R [SIGN+ D]) | Role R subsumes (Kleene-Dienes implication) the role chain R1 ... Rn with a degree SIGN+ D |
| (l-implies-role R1 R2 ... Rn R [SIGN+ D]) | Role R subsumes (Łukasiewicz implication) the role chain R1 ... Rn with a degree SIGN+ D |
| (equivalent-roles R1 R2) | R1 is equivalent to R2 |
| (inverse R1 R2) | R1 is inverse to R2 |
| (domain R C) | Equivalent to (implies (some R *top*) C) |
| (g-range R C) | Equivalent to (implies *top* (g-all R C)) |
| (z-range R C) | Equivalent to (implies *top* (z-all R C)) |
| (functional R) | R is functional |
| (inverse-functional R) | The inverse of R is functional |
| ([transitive | g-transitive | z-transitive] R) | R is transitive (Gödel-Zadeh conjunction) |
| (l-transitive R) | R is transitive (Łukasiewicz conjunction) |
| (symmetric R) | R is symmetric |
| (asymmetric S) | S is asymmetric |
| (reflexive R) | R is reflexive |
| (irreflexive S) | S is irreflexive |
| (disjoint-roles S1 .... Sn) | Roles S1 ... Sn are mutually disjoint |
| (crisp-role R) | R is crisp |